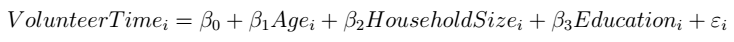Class Lab 8
Multivariate Regression
Review of Simple Linear Regression
In this lab, we extend our linear regression model to include more than one independent variable (X). In the simple linear model, we are interested in the relationship between X and Y. We assume a linear relationship in the population where each additional change in X has a corresponding change in Y. Since the relationship is linear, we can collect some data on X and Y from a sample and use the slope of the line between X and Y in our sample to draw inferences about the relationship in the broader population. That is, we are modeling:
\[Y_i = \beta_0 + \beta_1 X_i + \varepsilon_i\]and $\beta_1$ captures the relationship between X and Y. For this example, we will use data from the American Time Use Survey (ATUS) to look at time spent on volunteering (in minutes). We might think that as people get older, they spend more time volunteering because they have more discretionary time. We would then estimate the simple linear model:
\[VolunteerTime_i = \beta_0 + \beta_1 Age_i + \varepsilon_i\]by using the simple command:
reg volunteer_tot2 teage
and would get the results:
Source | SS df MS Number of obs = 146,562
-------------+---------------------------------- F(1, 146560) = 177.55
Model | 396879.313 1 396879.313 Prob > F = 0.0000
Residual | 327602931 146,560 2235.28201 R-squared = 0.0012
-------------+---------------------------------- Adj R-squared = 0.0012
Total | 327999810 146,561 2237.9747 Root MSE = 47.279
------------------------------------------------------------------------------
volunteer_~2 | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
teage | .1349619 .0101286 13.32 0.000 .1151101 .1548137
_cons | 3.134572 .4457724 7.03 0.000 2.260867 4.008277
------------------------------------------------------------------------------
In the output, just as before, the number of observations and $R^2$ can be found in the top-right. The $R^2$ suggests only about 0.12% of the variation in volunteering is explained by our simple linear model. The model suggests that every additional year in age corresponds with 0.13 additional minutes spent volunteering on an average day. The p-value is extremely low, suggesting the relationship is statistically significant. Note that this means every decade sees a 1.3 minute increase in daily volunteer time (0.13 x 10 = 1.3).
Multivariate Regressions
Of course, we know (or have good reason to believe) that other variables might also explain volunteering beyond age. Worse, some might be correlated with both age and time spent volunteering. For example, as people get older, they might live in large households with more people to care for in their family. Such family commitments might eat into the time available for volunteering. We will account for this with the simple model:
\[VolunteerTime_i = \beta_0 + \beta_1 Age_i + \beta_2 HouseholdSize_i + \varepsilon_i\]where household size is the number of people in the household. In Stata, estimating a multivariate linear regression is simple. You simply add the new independent variables $(X1, X2, X3,….Xk)$ to the code of the regression model used before with the format reg y x1 x2 x3 ... xk. In this case, we will run the code:
. reg volunteer_tot2 teage hhsize
Source | SS df MS Number of obs = 146,562
-------------+---------------------------------- F(2, 146559) = 201.21
Model | 898159.075 2 449079.537 Prob > F = 0.0000
Residual | 327101651 146,559 2231.87693 R-squared = 0.0027
-------------+---------------------------------- Adj R-squared = 0.0027
Total | 327999810 146,561 2237.9747 Root MSE = 47.243
------------------------------------------------------------------------------
volunteer_~2 | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
teage | .1833095 .0106226 17.26 0.000 .1624895 .2041296
hhsize | 1.27454 .0850449 14.99 0.000 1.107854 1.441226
_cons | -2.712517 .5921398 -4.58 0.000 -3.8731 -1.551935
------------------------------------------------------------------------------
A few things jump out. First, our model controlling for both household size and age explains more than twice the variation in volunteering time (the $R^2$ increased to 0.0027). Second, after account for household size, the relationship between age and volunteering time increased. This is consistent with what we thought before: as you age, you are more likely to have commitments at home that reduce your time for volunteering. Once we account for the effect of household size, we better isolate the increase in volunteering associated with age. Third, we can see that as household size grows, volunteering time increases. This could be because in really large families, there are additional hands to help at home while someone volunteers elsewhere or as children age new volunteering opportunities related to the child arise. Regardless, the results show that each additional household member is associated with a 1.27 minute increase in time spent volunteering on the average day. A 21 year old with a household of size 0 would be expected to volunteer for 1.07 minutes per day, on average, (-2.71 [cons or the intercept] + 0.18x21 + 1.27x0) or about 6.07 hours per year. Fourth, and finally, we can see that both coefficients have an associate standard error, t-statistic, p-value, and confidence interval. Here, both relationships are statistically significant, as the p-values suggest that very few samples of this size would have estimated relationships like these if the underlying relationship was actually zero.
Multivariate Regression with Categorical Variables
Sometime we might want to control for a categorical variable in our regression, which has a very different interpretation. For example, a person’s level of education probably correlates with both their age and how much time they spend volunteering. Multivariate regressions seek to account for additional factors to better isolate the the relationship between the independent variables (age and education) and the dependent variable (volunteer time).
One final note on multivariate regression. Recall that a binary variable in simple regression provide a difference in means between two groups. In multivariate regression, you can control for continuous variables, like age, directly, but for categorical variable, like educational attainment, you must control for all but one category separately. In doing so, the category not controlled for becomes $\beta_0$ (the intercept) and the coefficients for each category measure the conditional difference in means between that category and the omitted category. Our example will make this more clear.
As before, we will simply add a control for education to our regression code, addressing the additional nuance of controlling for a categorical variable in Stata. You can have Stata quickly create controls for each category in a categorical variable and omit a category to serve as the reference group by simply adding i. before the variable’s name in the code. We will add education to our model of volunteer time to model volunteering as the linear function:
Our measure of education is categorical and looks like this:
. tab peeduca
Edited: highest level of school |
completed or the highest degree |
received? | Freq. Percent Cum.
----------------------------------------+-----------------------------------
Less than 1st grade | 203 0.14 0.14
1st, 2nd, 3rd, or 4th grade | 748 0.51 0.65
5th or 6th grade | 1,856 1.27 1.92
7th or 8th grade | 1,815 1.24 3.15
9th grade | 2,085 1.42 4.58
10th grade | 2,399 1.64 6.21
11th grade | 4,051 2.76 8.98
12th grade - no diploma | 1,664 1.14 10.11
High school graduate - diploma or equiv | 37,563 25.63 35.74
Some college but no degree | 27,759 18.94 54.68
Associate degree - occupational/vocatio | 7,103 4.85 59.53
Associate degree - academic program | 8,024 5.47 65.00
Bachelor's degree (BA, AB, BS, etc.) | 32,706 22.32 87.32
Master's degree (MA, MS, MEng, MEd, MSW | 13,620 9.29 96.61
Professional school degree (MD, DDS, DV | 2,499 1.71 98.32
Doctoral degree (PhD, EdD, etc.) | 2,467 1.68 100.00
----------------------------------------+-----------------------------------
Total | 146,562 100.00
As you can see, there are categories that have different numbers of years of education together in the same category. In that case, an increase of one unit in the category does not always indicate a constant change in the number of years of education, so we cannot simply control for the education variable. We must control for each category of education either by adding a binary variable for each category and manually choosing one category to omit or by using the Stata command above. We will keep life simple and use the Stata command by using the code:
. reg volunteer_tot2 teage hhsize i.peeduca
Source | SS df MS Number of obs = 146,562
-------------+---------------------------------- F(17, 146544) = 57.85
Model | 2186696.76 17 128629.221 Prob > F = 0.0000
Residual | 325813114 146,544 2223.31254 R-squared = 0.0067
-------------+---------------------------------- Adj R-squared = 0.0066
Total | 327999810 146,561 2237.9747 Root MSE = 47.152
----------------------------------------------------------------------------------------------------------------
volunteer_tot2 | Coefficient Std. err. t P>|t| [95% conf. interval]
-----------------------------------------------+----------------------------------------------------------------
teage | .1818432 .0107206 16.96 0.000 .1608309 .2028554
hhsize | 1.403525 .0853421 16.45 0.000 1.236256 1.570793
|
peeduca |
1st, 2nd, 3rd, or 4th grade | -1.009009 3.731611 -0.27 0.787 -8.322893 6.304874
5th or 6th grade | .4138075 3.485945 0.12 0.906 -6.418575 7.24619
7th or 8th grade | 2.16827 3.489902 0.62 0.534 -4.671869 9.008409
9th grade | 1.364088 3.467362 0.39 0.694 -5.431872 8.160049
10th grade | 3.918561 3.44785 1.14 0.256 -2.839156 10.67628
11th grade | 5.252189 3.394038 1.55 0.122 -1.400059 11.90444
12th grade - no diploma | 5.940365 3.507427 1.69 0.090 -.9341221 12.81485
High school graduate - diploma or equivale..) | 5.295204 3.319563 1.60 0.111 -1.211074 11.80148
Some college but no degree | 7.625672 3.323263 2.29 0.022 1.112143 14.1392
Associate degree - occupational/vocational | 7.180665 3.357652 2.14 0.032 .5997339 13.7616
Associate degree - academic program | 9.069735 3.352349 2.71 0.007 2.499197 15.64027
Bachelor's degree (BA, AB, BS, etc.) | 10.96406 3.321156 3.30 0.001 4.454661 17.47346
Master's degree (MA, MS, MEng, MEd, MSW, e..) | 12.09648 3.335184 3.63 0.000 5.559583 18.63337
Professional school degree (MD, DDS, DVM, ..) | 9.449662 3.44208 2.75 0.006 2.703253 16.19607
Doctoral degree (PhD, EdD, etc.) | 13.32316 3.443903 3.87 0.000 6.573174 20.07314
|
_cons | -10.96062 3.376748 -3.25 0.001 -17.57898 -4.342261
----------------------------------------------------------------------------------------------------------------
Collectively, all of the coefficients for each category of education capture the parameter for education in the underlying model, $\beta_3$ from equation 4. Notice that the estimates generally get larger for each category of higher levels of educational attainment. There are a few things to note about this output. First, notice that the lowest category, “Less than 1st grade,” does not have a coefficient. That is because this is serving as the reference group. Thus, all coefficients on the education categories capture the estimated difference in average volunteering time between that category and the reference group, those with less than a 1st grade level of formal education. By way of example, the results show that people with a bachelor’s degree spend, on average, 10 more minutes volunteering than people of the same age with the same sized household but less than a 1st grade level of education. Second, adding education explains even more of the variation in volunteer time, as our $R^2$ more than doubles to 0.0067 (or 0.67%). Third, the difference in volunteering time per day between those with less than a 1st grade education level and other levels of education is not statistically significant until an education level of “Some college but no degree” (look at the p-values to confirm this). Finally, notice that the estimated coefficients for age did not change much, but there was some change in the effect of household size.